BLOG
SCOTT'S THOUGHTS

Advanced Assessment Methods: How to Apply Advanced Assessment
In my last blog, I discussed the use of stepwise regression, in which possible predictor variables are entered into a regression model until the best statistically significant variables are determined. I want to resume this discussion today by looking at some real-life examples of predictor variables and how they were determined.
Example 1
For a 2020 cohort, EORE and the number of remediations were the statistically significant (p < 0.01) predictors remaining in the model. A combination of these variables was the best predictor of PANCE scores. With enough data, you can begin to identify a Multiple Variable Risk Model. The multiple correlation coefficient (correlation between PANCE scores predicted by the model and actual PANCE scores) for this final model was high (R =0.76). The variables (EORE and number of remediations) explained 58.3% of the variance in PANCE scores
Example 2
For a 2020 cohort, the EORE, History and Physical I, Clinical Medicine I, Clinical Problem Solving I, SUMM II, and Undergrad GPA were the statistically significant (p < 0.05) predictors remaining in the model. The multiple correlation coefficient (correlation between PANCE scores predicted by the model and actual PANCE scores) for this final model was very high (0.95). These variables explain a large amount of the variance (89.8%) in PANCE scores.
Usefulness of Regression Modeling
To summarize, regression modeling provides the following benefits:
Correlational analysis can identify individual predictor variables associated with an outcome variable such as PANCE scores. Regression modeling goes further by yielding an equation to predict future PANCE scores from a predictor variable
Regression equations for statistically significant predictors can then be used to predict PANCE scores and identify at-risk students for interventions
Stepwise regression analysis also used separately with the data from didactic and clinical year variables
Of note, regression modeling can be performed with PANCE outcome (low/high score) as the predicted variable and PACKRAT, PACKRAT II, EORE and EOC as predictor variables in separate analyses. For example, a cut-off of a PANCE score of less than 400 or 350 can classify candidates as having a low score. The outcome variable will be coded as 1 for a low PANCE score since the emphasis of the analysis is on identifying candidates needing remediation based on a low predicted future PANCE score.
Changing Policy?
Can you create predictions that lead to policy-defining events?
Oftentimes, programs struggle, wondering “Where do we set our benchmark?” Predictor variables are an excellent way to gauge the answer to that question.

In this data set, I took 416 individuals, and I ran binary logistic regression. I wanted to see, based on my data with these exams, what the predictor factor was.
I applied the Receiver Operating Characteristic Curve (ROC), a technique for summarizing classifier performance over a range of trade-offs between true positive and false positive error rates. It helps identify probability factors. My statistician helped me to better understand this, but I will give you the quick and straightforward way of looking at it.
Based on the ROC curves, specificity and sensitivity for all models were calculated under various probability cut-off values. In other words, analyses determined what the sensitivity and specificity values would be if different probability cut-off values are selected for classifying a record as a PANCE outcome of low score.

So why look at this? I feel like in years past, it was believed that a 140 PACKRAT score was not too bad – but these results tell a different story. This says that a 140 PACKRAT still puts students squarely in a high-risk zone for failing the PANCE.
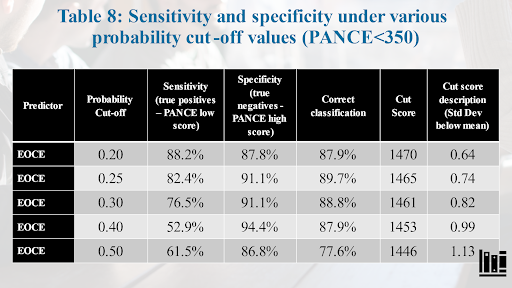
I did the same for the End of Curriculum Exam. There was a robust amount of data – seventeen individuals out of 107 that did not pass the PANCE. This is compelling data.
What is the score at or below that has a 50% probability of failing the PANCE? That is 1446. If you go all the way up to 1470, that is still a 20% chance. My intention is not to criticize PAEA standards, but PAEA sets a benchmark of 1400 as being the minimum “safe” score, while the data we see here shows that is not the case – in fact, you may need to think of your cut scores as being a bit higher. When I showed this data to programs, it often resulted in the adoption of higher benchmarks.
In another case, after looking at a similar model on EORE scores, a program raised the first-time taker EORE requirement from 70% to 75%, which is definitely a data-driven approach.
I hope this section of blogs about interpreting advanced assessment methods have been helpful to you. In my next blog, I will begin a new section regarding the use of advanced assessment to form a risk model that will improve your PA program’s ability to select the best students and give them their best chances at first-time PANCE pass rates, while also lowering your attrition rates. It will be worth coming back for, so I will see you then.

Advanced Assessment Methods: How to Apply Advanced Assessment
In my last blog, I discussed the use of stepwise regression, in which possible predictor variables are entered into a regression model until the best statistically significant variables are determined. I want to resume this discussion today by looking at some real-life examples of predictor variables and how they were determined.
Example 1
For a 2020 cohort, EORE and the number of remediations were the statistically significant (p < 0.01) predictors remaining in the model. A combination of these variables was the best predictor of PANCE scores. With enough data, you can begin to identify a Multiple Variable Risk Model. The multiple correlation coefficient (correlation between PANCE scores predicted by the model and actual PANCE scores) for this final model was high (R =0.76). The variables (EORE and number of remediations) explained 58.3% of the variance in PANCE scores
Example 2
For a 2020 cohort, the EORE, History and Physical I, Clinical Medicine I, Clinical Problem Solving I, SUMM II, and Undergrad GPA were the statistically significant (p < 0.05) predictors remaining in the model. The multiple correlation coefficient (correlation between PANCE scores predicted by the model and actual PANCE scores) for this final model was very high (0.95). These variables explain a large amount of the variance (89.8%) in PANCE scores.
Usefulness of Regression Modeling
To summarize, regression modeling provides the following benefits:
Correlational analysis can identify individual predictor variables associated with an outcome variable such as PANCE scores. Regression modeling goes further by yielding an equation to predict future PANCE scores from a predictor variable
Regression equations for statistically significant predictors can then be used to predict PANCE scores and identify at-risk students for interventions
Stepwise regression analysis also used separately with the data from didactic and clinical year variables
Of note, regression modeling can be performed with PANCE outcome (low/high score) as the predicted variable and PACKRAT, PACKRAT II, EORE and EOC as predictor variables in separate analyses. For example, a cut-off of a PANCE score of less than 400 or 350 can classify candidates as having a low score. The outcome variable will be coded as 1 for a low PANCE score since the emphasis of the analysis is on identifying candidates needing remediation based on a low predicted future PANCE score.
Changing Policy?
Can you create predictions that lead to policy-defining events?
Oftentimes, programs struggle, wondering “Where do we set our benchmark?” Predictor variables are an excellent way to gauge the answer to that question.

In this data set, I took 416 individuals, and I ran binary logistic regression. I wanted to see, based on my data with these exams, what the predictor factor was.
I applied the Receiver Operating Characteristic Curve (ROC), a technique for summarizing classifier performance over a range of trade-offs between true positive and false positive error rates. It helps identify probability factors. My statistician helped me to better understand this, but I will give you the quick and straightforward way of looking at it.
Based on the ROC curves, specificity and sensitivity for all models were calculated under various probability cut-off values. In other words, analyses determined what the sensitivity and specificity values would be if different probability cut-off values are selected for classifying a record as a PANCE outcome of low score.

So why look at this? I feel like in years past, it was believed that a 140 PACKRAT score was not too bad – but these results tell a different story. This says that a 140 PACKRAT still puts students squarely in a high-risk zone for failing the PANCE.

I did the same for the End of Curriculum Exam. There was a robust amount of data – seventeen individuals out of 107 that did not pass the PANCE. This is compelling data.
What is the score at or below that has a 50% probability of failing the PANCE? That is 1446. If you go all the way up to 1470, that is still a 20% chance. My intention is not to criticize PAEA standards, but PAEA sets a benchmark of 1400 as being the minimum “safe” score, while the data we see here shows that is not the case – in fact, you may need to think of your cut scores as being a bit higher. When I showed this data to programs, it often resulted in the adoption of higher benchmarks.
In another case, after looking at a similar model on EORE scores, a program raised the first-time taker EORE requirement from 70% to 75%, which is definitely a data-driven approach.
I hope this section of blogs about interpreting advanced assessment methods have been helpful to you. In my next blog, I will begin a new section regarding the use of advanced assessment to form a risk model that will improve your PA program’s ability to select the best students and give them their best chances at first-time PANCE pass rates, while also lowering your attrition rates. It will be worth coming back for, so I will see you then.
Don't miss out on future events!
Subscribe to our newsletter

© 2025 Scott Massey Ph.D. LLC

